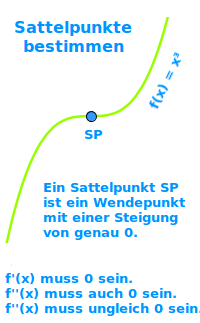
Sattelpunkte bestimmen
15 Aufgaben mit Lösungen
Finde zu jeder Funktion die Sattelpunkte. Es kann sein, dass eine Funktion keinen, einen oder auch mehrere Sattelpunkte hat. Gibt die Lösung in Form von Punkten (x|y) an.
a) f(x) = x
c) f(x) = x³
d) f(x) = x^4
e) f(x) = x^5
f) f(x) = 2x^5+5x^4-10x³-20x²+40x+30
g) f(x) = x^5-5x^4+5x³+1
h) f(x) = x³-3x²+3x+7
i) f(x) = 2x³-6x²+6x
j) f(x) = x^5+5x^4+5x^3-1
k) f(x) = x(4-x)³
l) f(x) = 4(x-1)³+(x-1)^4
m) f(x) = (x-4)³
n) f(x) = x³-12x²+48x-64
o) f(x) = 2x⁵+5x⁴-10x³-20x²+40x+30
Lösungen
a) keine SP
b) keine SP
c) (0|0)
d) keine SP
e) (0|0)
f) (-2|-34) und (1|4)
g) (0|1)
h) (1|8)
i) (1|2)
j) (0|-1)
k) (4|0)
l) (1|0)
m) (4|0)
n) (4|0)
o) (-2|-34) und (1|47)