Teiler
Definition
© 2016
- 2026
Basiswissen
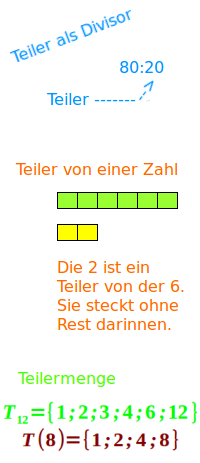
Das Wort Teiler hat mehrere Bedeutungen: es gibt die Teiler einer Zahl, es gibt die Teilermenge (alle Teiler zusammen) sowie auch den Teiler als Divisor. Diese Bedeutungen werden kurz erklärt.
Teiler einer Zahl
- Ein Teiler gehört immer zu einer ganzen Zahl, die wir z nennen.
- Ganze Zahlen sind zum Beispiel die -4, -3, -2, -1, 0, 1, 2, 3 etc.
DEFINITION:
"Will man die Teiler einer Zahl ermitteln […], so ist ein einfaches und sicheres Verfahren, alle Teiler zu finden, die Zahl nacheinander durch 1, 2, 3 … usw. zu dividieren. Geht die Division ohne Rest auf, so hat man einen Teiler gefunden." [3]
"Will man die Teiler einer Zahl ermitteln […], so ist ein einfaches und sicheres Verfahren, alle Teiler zu finden, die Zahl nacheinander durch 1, 2, 3 … usw. zu dividieren. Geht die Division ohne Rest auf, so hat man einen Teiler gefunden." [3]
- Natürliche Zahlen fangen erst mit der 1 an: 1, 2, 3, 4, 5 etc.
- Ein Teiler von z ist immer ganzzahlig und steckt ohne Rest in z.
- Die Zahl 1 ist immer ein Teiler. Sie heißt "trivialer Teiler". [3]
- Die Zahl z selbst ist immer auch ihr eigener "trivialer" Teiler. [3]
- Solche Teiler von der 8 wären die 1, die 2, die 4 und die 8 selbst.
- Mehr dazu unter 👉 Teiler einer Zahl
Teiler als Teilermenge
- Teiler als Mehrzahl meint die Teiler einer Zahl.
- Die Teiler von der 8 sind 1; 2; 4 und die 8 selbst.
- Mehr dazu unter 👉 Teilermenge
Teiler als Divisor
- Jede Zahl, durch die man teilt, kann man Teiler nennen.
- Das Fremdwort für Teiler ist "Divisor".
- Bei 8:4 wäre die 4 der Teiler oder Divisor.
- (Die 8 nennt man Dividend.)
- Mehr unter 👉 Teiler als Divisor
Fußnoten
- [1] Teiler. In: Spektrum Lexikon der Mathematik. Dezember 2021. Online: https://www.spektrum.de/lexikon/mathematik/teiler/10269
- [2] Teiler in einem Lexikon aus dem Jahr 1910, mathematisch: "Teil, aliquoter, in der Arithmetik ein Divisor, durch welchen das Ganze ohne Rest teilbar ist. Jeder andre Teil, mit welchem ein Ganzes nicht ohne Rest teilbar ist, heißt aliquanter Teil. So sind z.B. 2, 3, 4, 6 aliquote, 5, 7, 8, 9 aliquante Teile von 12." In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 8 Stuttgart, Leipzig 1910., S. 429. Online: http://www.zeno.org/nid/20006139159
Fußnoten
- [1] Teiler. In: Spektrum Lexikon der Mathematik. Dezember 2021. Online: https://www.spektrum.de/lexikon/mathematik/teiler/10269
- [2] Teiler in einem Lexikon aus dem Jahr 1910, mathematisch: "Teil, aliquoter, in der Arithmetik ein Divisor, durch welchen das Ganze ohne Rest teilbar ist. Jeder andre Teil, mit welchem ein Ganzes nicht ohne Rest teilbar ist, heißt aliquanter Teil. So sind z.B. 2, 3, 4, 6 aliquote, 5, 7, 8, 9 aliquante Teile von 12." In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 8 Stuttgart, Leipzig 1910., S. 429. Online: http://www.zeno.org/nid/20006139159
- [3] Wolfang Crayaufmüller: Primzahlfamilien. Selbstverlag. 1995. ISBN: 3-9801032-2-6. Dort im Kapitel "Zahlenfamilien", Seite 7. Siehe auch
- [4] "Die Teiler, die jede Zahl n hat, nämlich 1 und n heißen triviale Teiler." In: Wolfang Crayaufmüller: Primzahlfamilien. Selbstverlag. 1995. ISBN: 3-9801032-2-6. Dort im Kapitel "Zahlenfamilien", Seite 7. Siehe auch