Basiswissen

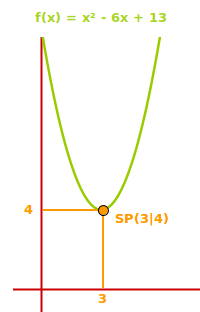
f(x) = x²-6x+13 ist eine Gleichung einer quadratischen Funktion in Normalform, auch Parabelgleichung genannt. Mit Hilfe der sogenannten quadratischen Ergänzung kann man dafür den Scheitelpunkt bestimmen. Das ist hier Schritt-für-Schritt erklärt.

Bildbeschreibung und Urheberrecht — Man sieht den Graphen von: f(x) = x² - 6x + 13☛

Worum geht es bei dieser Methode?

Es geht um die Bestimmung des Scheitelpunktes von quadratischen Funktionen.

Oft hat man aber von der Funktion erst einmal die Normalform gegeben.

Aus ihr kann man den Scheitelpunkt nicht direkt ablesen.

Man kann die Normalform aber umwandeln in die sogenannte Scheitelpunktform.

Aus ihr kann man dann den Scheitelpunkt direkt ablesen.

Dazu ist hier das Verfahren mit der Quadratischen Ergänzung (QE) erkkärt.

Dieses Verfahren wird von vielen Lernenden nur schwer erlernt.

Es kommt in den höheren Schulklassen meist nicht mehr vor.

Siehe als Grundwissen auch quadratische Ergänzung ↗

Was ist das Ziel?

Gegeben: Normalform, z. B.: f(x) = x² - 6x + 13

Gesucht: Scheitelpunktform: f(x) = a(x-d)² + e

1. Quadratische Ergänzung
1. Normalform hinschreiben: f(x) = x² - 6x + 13
1. Zahl vor x halbieren und dann quadrieren gibt hier: 9
1. Dieses Ergebnis dann einmal mit + und einmal mit - hinschreiben:
1. f(x) = x² - 6x + 9 - 9 + 13

2. Einklammern
2. Aus den ersten drei Gliedern wird eine Klammer mit ² gemacht:
2. Ergebnis aus Schritt 1 notieren: f(x) = x² - 6x + 9 - 9 + 13
2. Dann in Zeile darunter immer hinschreiben: f(x) = (x
2. Dann die Zahl vor dem x halbieren, Vorzeichen mitnehmen:
2. Im Beispiel halbiert man also die -6 und daraus wird -3.
2. Das wird jetzt hinter das x geschieben: f(x) = (x-3
2. Dann die Klammer schließen und ² schreiben: f(x) = (x-3)²
2. Dann die zwei letzten Zahlen ohne x aus Schritt 1 zusammenfassen:
2. Im Beispiel wäre das: -9+13, das gibt: +4
2. Das am Ende des neuen Terms anfügen:
2. f(x) = (x-3)² + 4

3. Scheitelpunkt ablesen
3. Das Ergebnis aus Schritt 2 heißt Scheitelpunktform.
3. Zuerst wird der x-Wert des Scheitelpunktes bestimmt:
3. Nimm dazu die Zahl nach dem x in der Klammer, hier also die -3.
3. Drehe davon das Vorzeichen um, aus -3 wird also +3 oder kurz 3.
3. Das ist der x-Wert des Scheitelpunktes.
3. Der y-Wert ist immer die Zahl nach der Klammer, hier also: +4.
3. Scheitelpunkt aufschreiben gibt: SP(3|4) ✔