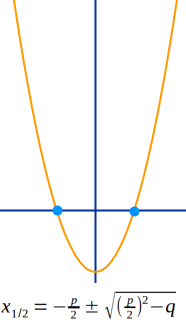
Nullstellen von reinquadratischen Funktionen über pq-Formel
f(x) = 3x² - 27
© 2017
- 2025
Basiswissen
Reinquadratisch nennt man eine Gleichung, wenn man sie umformen kann in 0 = ax²+b. Das b darf auch die Zahl 0 sein oder negativ. Das a darf jede Zahl außer der 0 sein. Solche Gleichungen kann man immer mit der pq-Formel lösen. Das ist hier mit einem Beispiel und Übungsaufgaben kurz vorgestellt.
Vorbereitung
- Setze f(x) zuerst immer gleich 0. Das gibt: 0 = 3x² - 27
- pq-Formel geht nur für die Normalform x² + px + q
- Also die Funktionsgleichung erst in Normalform bringen:
- Ergänze das fehlende lineare Glied (nur mit x), das gibt:
- Teile durch a, das gibt: 0 = x² - 9
- Ergänze fehlendes Lineareglied, gibt:
- 0 = x² + 0x - 9
pq-Formel
- p und q ablesen, Achtung: Vorzeichen gehört dazu:
- p = 0 und q = -9
- In pq-Formel einsetzen gibt:
- 1. NS bei: -0/2 + Wurzel [0²-(-9)]
- 2. NS bei: -0/2 - Wurzel [0²-(-9)]
- NS bei 3 und -3
Aufgaben dazu
- Übungsaufgaben mit Lösungen unter => qck