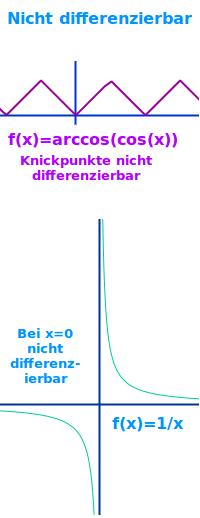
Nicht differenzierbar
Meint: man kann keine Ableitung bilden.
© 2016
- 2025
Basiswissen
Differenzieren heißt ableiten, also f'(x) bilden. Nicht jede mathematische Funktion ist an allen Stellen differenzierbar: an Ecken, Lücken und Sprüngen kann man zum Beispiel keine Ableitung bilden. Anschaulich heißt das: an einem Punkt lässt sich nicht eindeutig eine Tangente anlegen.
Definition
- Differenzieren ist ein anderes Wort für ableiten.
- Nicht differenzierbar heißt also "nicht ableitbar".
- Ableiten heißt, eine Funktion für alle Steigungen eines Graphen zu finden.
- Dass man Ableiten kann, muss die Funktion eindeutigen Steigungen haben.
- Es gibt Stellen an Graphen, an denen die Steigung nicht eindeutig ist.
- Wo der Graph eine Lücke hat, ist die Steigung nicht definiert.
- Wo der Graph einen Knick hat, ist die Steigung nicht definiert.
- Wo der Graph einen Sprung hat, ist die Steigung nicht definiert.
- An solchen Stellen ist die Funktion nicht differenzierbar.
Beispiele
- Die Zickzack-Funktion f(x)=arccos(cos(x)) hat mehrere Knicke.
- Die Betragsfunktion f(x)=|x| an der Stelle x=0
- Die Normalhyperbel f(x)=1:x an der Stelle x=0
- Die Heaviside-Funktion an der Stelle x=0
- Jede 👉 Sprungstelle