McCulloch-Pitts-Neuron

Physik

Definition｜ Rechengang｜ Eigenschaften｜ Rechenbeispiel｜ Analogien zu menschlicher Informationsarbeit?｜ Verdichtung｜ Verzweigter Output｜ Feste Kanäle｜ Wichtung der Kanäle｜ Desiderata｜ Fußnoten

Definition

Ein McCulloch-Pitts-Neuron, auch McCulloch-Pitts-Zelle, kurz MCP ist ein sehr begrenztes mathematisches Modell zur Simulation vermuteter Eigenschaften realer Nervenzellen im Gehirnen. Das Model wurde im Jahr 1943 vorgeschlagen. Es war der Beginn der Entwicklung künstlicher neuronaler Netze.

Bildbeschreibung und Urheberrecht — Kann man sich ein Dreieck vorstellen, dessen längste Seite noch länger ist als die zwei kürzeren Seiten zusammen an Länge haben? Falls nicht, ist die Erkenntnis, dass die längste Seite niemals länger als die Summe der Längen der zwei anderen Seiten sein kann eine Erkenntnis a priori (ohne Erfahrung!) im Sinne von Kant? © Gunter Heim/Gemini (KI) ☛

Rechengang

Nᵢ(t+1) = H[Σwᵢⱼ(t)Nⱼ(t)-θ(t)]

Legende

Nᵢ(t+1) = der Zustand (Ausgabe) des i-ten Neurons zum Zeitpunkt t, entweder 0 oder 1

H = für negative Zahlen 0, für alle anderen 1, die 👉 Heaviside-Funktion

Σ = Summenzeichen, hier von j=1 bis zum letzten j 👉 Summenzeichen

Nⱼ = er Zustand (Ausgabe) des j-ten Neurons zum Zeitpunkt t

wᵢⱼ = Gewicht des Signals zum Neuron i vom Neuron j, nur ganze Zahlen

θ(t) = der Schwellenwert zum Zeitpunkt t, nur ganze Zahlen

Eigenschaften

Jedes Neuron hat keinen oder mehrere Eingänge (inputs)

Jeder Eingang kann entweder erregend oder hemmend wirken.

Die Ausgabe (output) ist entweder "Feuern" oder gar nichts. (1 oder 0).

Jedes Neuron hat einen internen Schwellenwert.

In einem Netzwerk arbeiten die Neuronen in diskreten Zeitschritten.

Die Neuronen arbeiten synchron innerhalb eines Zeitabschnitts.

Jede Ausgabe kann zu beliebig vielen Eingaben anderer Neuronen werden.

Ein Neuron kann seine Ausgabe auch als Eingabe (im nächsten Zeitschritt) für sich selbst haben.

Eine Ausgabe kann höchstens einmal mit einem anderen Zielneuron verbunden sein.

Rechenbeispiel

In der originale Veröffentlichung von 1943 verwendeten McCullochs und Pitts nur ganze Zahlen als Gewichte. Als Gewichte w möglichen waren also Werte wie -7, -1, 0, 2 oder 9. Der Output eines Neurons war immer entweder 0 oder 1. Der Schwellenwert konnte ebenfalls eine beliebige ganze Zahl sein.

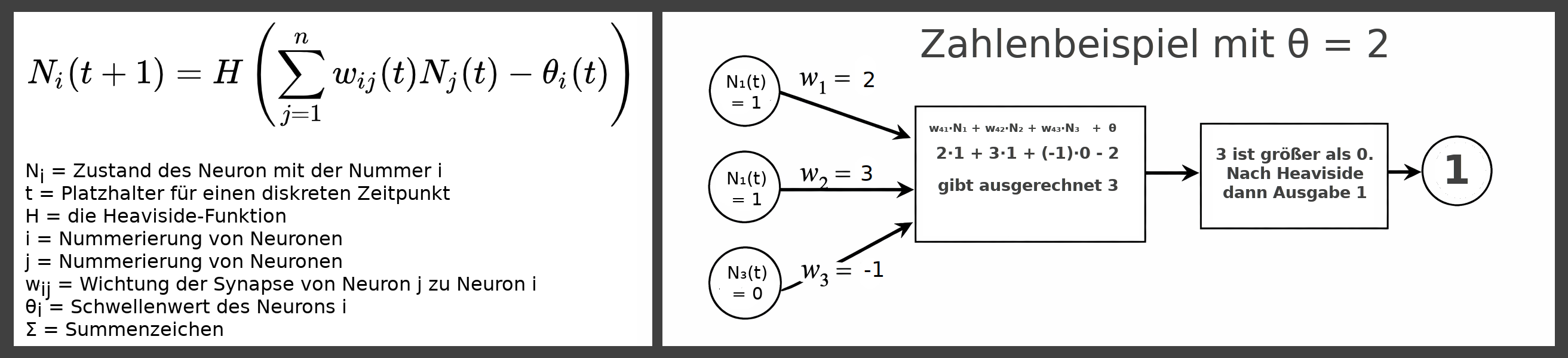
Wir betrachten als einfaches Beispiel ein Netzwerk aus 4 Neuronen. Die ersten drei Neuronen, nummeriert mit i=1, i=2 und i=3 haben nur Ausgänge. Jedes dieser Neuronen kann feuern oder nicht feuern, also als Output entweder 1 oder 0 geben. Man kann mit diesem drei Neuronen also die binären Zahlen 000, 001, 010, 011, 100, 101, 110 und 111 modellieren. Das sind die ganzen Zahlen von 0 bis 7.

Von jedem dieser drei Neuronen i=1, i=2 und i=3 geht je eine Verbindung zum vierten Neuron i=4. Die Schreibweise wij ist das Gewicht der Verbindung vom Neuron j zum Neuron i. Man kann dann für das vierte Neuron die Gewichte der drei eingehenden Verbindungen mit beispielhaften Werten belegen:

w₄₁ = 2

w₄₂ = 3

w₄₃ = -1

w₄₁·N₁ w₄₂·N₂ + w₄₃·N₃ + θ

Und als Schwellenwert z. B.

θ = 2

Und beispiehlaften Anfangwerten

N₁(t) = 1

N₂(t) = 1

N₃(t) = 0

Mit der Formel:

Nᵢ(t+1) = H[Σwᵢⱼ(t)Nⱼ(t)-θ(t)]

Für Neuron i=4 einsetzen:

N₄(t+1) = H^{[1·2+3·1+(-1)·0 - 2]} | vereinfachen

N₄(t+1) = H^{[5 - 2]} | vereinfachen

N₄(t+1) = H^[3] | 👉 Heaviside-Funktion

N₄(t+1) = 1

Das heißt bei den gegebenen Anfangswerten für die Neuronen 1 bis 3 und dem gegebenen Gewicht θ im Neuron 4 feuert das Neuron 4. Man kann dann für alle möglichen Variationen der Anfangswerte die Ausgabe des vierten Neurons, des Output-Neurons des Netzes sozusagen berechnen. Kann man dem Output eine Bedeutung zurodnen? Hier erst einmal die Liste. Die ersten drei Zahlen sind jeweils der Input der Neuronen 1 bis 3, dann folgt der Output des Neurons 4:

0 0 0 (Dezimal 0) -> 0

0 0 1 (Dezimal 1) -> 0

0 1 0 (Dezimal 2) -> 1

0 1 1 (Dezimal 3) -> 1

1 0 0 (Dezimal 4) -> 1

1 0 1 (Dezimal 5) -> 0

1 1 0 (Dezimal 6) -> 1

1 1 1 (Dezimal 7) -> 1

Gäbe es den Output 0 nicht für die Eingabe 101 (Dezimal 5), könnte man sagen, das Netz feuert bei Eingaben größer als Dezimal 1 und bleibt ansonste ruhig. Die interessante Frage ist nun, ob man die Gewichte so verändern könnte, dass das Netz bei jeder eingegebenen Zahlgrößer 1 feuert und ansonste ruhig bleibt. Man kann "von Hand" probieren oder überlegen, ob man einen Algorithmus ersinnt, der die Gewichte so anpasst, dass der gewünschte Output ensteht. Damit kommt man zu dem Gedanken, die Netze nicht starr zu programmieren, sondern sie zu trainieren.

McCulloch und Pitts untersuchten bereits in den 1940er Jahren intenstiv, welche Art von Fragen oder Problemen ihre Neuronen und daraus gebaute Netze lösen können.

Spätere Entwicklungen ersetzten die Heaviside-Funktion durch andere Funktionen etwa eine Sigmoidfunktion (Schwanenhalskurve). Und Signale und Gewichte wurde später auch nicht mehr nur durch ganze sondern reelle Zahlen angegeben. Und vor allem wuchsen die künstliche Neuronalen Netze ins quasi unermessliche an.^[4]

Analogien zu menschlicher Informationsarbeit?

Ein McCulloch-Pitts-Neuron und alle von ihm abgeleiteten Neuronen haben einige zunächst erst einmal nur rein äußerliche Analogien zu typisch menschlicher Informationsarbeit in zielorientierten Organisationen, etwa großen Unternehmen, militärischen Einrichtungen oder Behörden.

Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.

Welche mehr als nur rein äußerlichen Ähnlichkeiten könnte es zwischen der Funktionsweise menschlicher Informationsarbeiter und einem künstliche Neuron geben?

Verdichtung

Aus einer großen Anzahl von einlaufenden Informationen wird als Ergebnis eine einzige, verdichtete Ausgabe gemacht. Man stelle sich etwa die Mitarbeiterin in der Kreditabteilung einer Bank vor. Als Output für eine konkrete Aufgabe soll sie nur ein "Ja" oder "Nein" abgeben, nämlich auf die Frage, ob man einem bestimmten Bittsteller für einen privaten Konsumkredit diesen Kredit gewähren soll oder nicht.

Sie verarbeitet dazu möglicherweise eine große Anzahl einlaufender Informationen: Bonitätshistorie des Bittstellers, Zuverlässigkeit des gegenwärtigen Arbeitgebers, Schufa-Auskünfte, zu erwartendes Zinsniveau der nächsten Jahre, interne Richtlinien der eigenen Bank, Vorgaben eines Qualitätsmanagements, Prüfungsberichte der Rechtsabteilung etc. etc. Die Klage vieler realer menschlicher Informationsarbeiter, man wisse oft nicht, was man eigentich den ganzen Tag über geleistet hätte, kann einen Ursprung darin haben, dass effiziente Informationsarbeit vielleicht gerade in der "Vernichtung" irrelevanter Information bis hin zu einem minimalistischen digitalen Output wie in einer Ja-Nein-Entscheidung bestehen könnte. Man sieht am Ende eines Arbeitstages kann geschaffenes Werk sondern im Idealfall so gut wie gar nichts.

Verzweigter Output

Der Output wird innerhalb einer realen Organisation in oft gleicher Weise an viele weitere Adressaten gerichtet. Die klassische technische Umsetzung sind Verteiler, etwa für Vermerke oder E-Mails. In biologischen Netzwerken entspräche das der Verzweigung eines ausgehenden Axons in viele Verzweigungen hin zu vielen anderen Zielneuronen.

Feste Kanäle

Wie die Verbindungen zwischen verschiedenen Neuronen in einem künstlichen neuronalen Netz sind die Informationsflüsse in menschlichen Organisationen oft eng kanalisiert. Nicht umsonst spricht man von Informationskanälen, etwa auch in sozialen Medien (Kanal abonnieren). Mitteilungen von Kunden kommen heute oft über ein Kundenkonto, allgemeine Richtlinien der Bank findet man auf einer bestimmten Webseite, Kommentare für einer Führungskraft kommen über deren E-Mail-Kanal, informelle Informationen über den Kanal "Kaffeeküche" etc. Mit etwas Phanatasie lassen sich viele weitere Beispiele finden.

Wichtung der Kanäle

Eine Mitareiterin in einer menschlichen Organisationen kann die Wahrscheinlichkeit mit der sie Informationen über bestimmte Kanäle erhält aktiv verändern, also wichten: man kann die Tür zum eigenen Büro offen halten oder schließen und damit Kollegen das Maß der Offenheit signalisieren, kommunizieren zu wollen, man kann E-Mails als gelesen oder ungelesen markieren, Lesemarken setzen oder auch nicht, Briefe in einem Stapel weiter nach oben oder weiter nach unten legen und so weiter. Zunehmend nehmen Algorithmen diese Wichtung im Hintegrund vor. Man denke beispielsweise an die Algorithmen sozialer Netzwerke, die sehr konkret die Informationen auswählen, die uns erreichen oder nicht. Je weiter unten in einer Scroll-Liste etwas steht, desto niedriger wird die dort verlinkte Information am Ende "ins Gewicht fallen".

Desiderata

Bei all diesen Analogien bleibt eine essentiell wichtige Eigenschaft künstlicher neuronaler Netze in der Übertragung auf biologische und organisationel Netzwerke ungeklärt: wie lernen biologische Netzwerke? Nach welchen Regeln ändern echte Nervenzellen die Gewichte an ihren Synapsen? Und wie wie könnte die Wichtung von Informationskanälen in menschlichen Organisationen gezielt so gesteuert werden, dass die Organisation als Ganzes in der Erfüllung ihrer Aufgaben besser wird? Siehe mehr zu dieser Spekulation im Artikel 👉 neuronale Organisation

Fußnoten

[1] Warren S. McCulloch, Walter Pitts: A logical calculus of the ideas immanent in nervous activity. The Bulletin of Mathematical Biophysics. 5 (4): 115–133. 1943. ISSN 0007-4985. Online: https://link.springer.com/article/10.1007/BF02478259

[2] Walter Pitts (1923 bis 1969) brachte sich als Kind und Autodidakt mehrere Sprachen wie Griechisch und Latein bei und las unter anderem die mathematischen Werke von Russel und Whitehead. Im Alter von 12 Jahren begann er ein Studium.

[3] Die Heaviside-Funktion ordnet jeder Zahl kleiner als 0, also jeder negativen Zahl, den Wert 0 zu. Jeder anderen Zahl, also auch der 0 selbst, wird dann der Wert 1 zugeordnet.

[4] Netze mit zum Beispiel 650.000 Neuronen werden beschrieben in: Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton: ImageNet classification with deep convolutional neural networks. Communications of the ACM. 60 (6): 84–90. doi:10.1145/3065386. ISSN 0001-0782. S2CID 195908774. Veröffentlicht im Jahr 2017. https://dl.acm.org/doi/10.1145/3065386Online: