A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

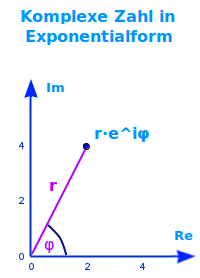
Komplexe Zahl in Exponentialform

Definition

© 2016 - 2025


Basiswissen｜ Legende｜ Umwandlungen｜ Rechenarten damit


Basiswissen


z = r mal e hoch (i mal phi) oder kurz geschrieben als r·e^iφ ist die Exponentialform einer komplexen Zahl. Mit dieser Darstellung lassen sich vor allem gut die Multiplikation und Division durchführen. Das ist hier kurz erklärt.



Bildbeschreibung und Urheberrecht
Eine komplexe Zahl allgemein dargestellt in Exponentialform: das r heißt der Betrag und ist anschaulich der Abstand der als Punkt gedachten komplexen Zahl vom Koordinatenursprung. Das kleine φ heißt Argument und ist der Winkel des Ortsvektors zum gedachten Punkt mit der reellen Achse.☛


Legende


  • z = die komplexe Zahl
  • r = Betrag der Zahl, Abstand zum Ursprung
  • e = Eulersche Zahl, etwa 2,71828
  • i = Imaginäre Einheit
  • phi = Argument der komplexen Zahl

Umwandlungen



Rechenarten damit