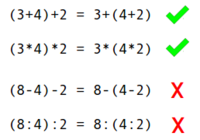Basiswissen

Aussage des Assoziativgesetzes allgemein

• Aufgaben, bei denen nur plus gerechnet wird heißen Plusketten.
  

• Aufgaben, bei denen nur mal gerechnet wird heißen Malketten.
  

• Bei reinen Plus- und bei reinen Malketten sind Klammern egal.
  

• Man kann Klammern immer setzen, weglassen oder verschieben.
  

• Egal was man mit den Klammern macht, es kommt immer dasselbe raus.
  

• Man sagt: Addition (plus) und Multiplikation (mal) sind assoziativ.
  

Das Assoziativgesetz für die Addition

• Angewandt auf die Addition, kann man sagen:
  

• Summenden können in beliebiger Reihenfolge zur Teilsummen verbunden werden^[1]
  

• Es gilt also zum Beispiel: 3+(4+5) = (3+4)+5 = (3+5)+4
  

• Man kann auch sagen: "In einer Summe aus drei oder mehr Zahlen darf man Klammern beleibig setzen oder weglassen. Dabei ändert sich der Wert der Summe nicht."^[3]
  

Das Assoziativgesetz für die Multiplikation

• Angewandt auf die Multiplikation, kann man sagen:
  

• Faktoren können in beliebiger Reihenfolge zur Teilprodukten verbunden werden^[2]
  

• Es gilt also zum Beispiel: 3·(4·5) = (3·4)·5 = (3·5)·4
  

• Man kann auch sagen: "In einem Produkt aus drei odre mehr Zahlen darf man Klammern beliebig setzen oder weglassen. Dabei ändert sich der Wert des Produktes nicht."^[3]
  

Was hat das mit dem Kommutativgesetz zu tun?

• Bei Plus- und Malketten macht die Rechenreihenfolge keinen Unterschied am Ergebnis.
  

• Also kann man die Zahlen vertauschen wie man will (Kommutativgesetz).
  

• Oder man kann Klammern setzen wie man will (Assoziativgesetz).
  

• Vertauschen oder Klammern setzen ändert die Rechenreihenfolge.
  

• Aber das ist bei Plus oder Mal vom Ergebnis her egal.
  

Beispiel für plus

• 3+4+2 = 9
  

• (3+4)+2 = 9
  

• 3+(4+2) = 9
  

Beispiel für mal

• 3·4·2 = 24
  

• (3·4)·2 = 24
  

• 3·(4·2) = 24
  

Wo gilt das Gesetz nicht?

• Bei der Subtraktion (minus)
  

• Bei der Division (geteilt)
  

• Beim Potenzieren (hoch)
  

• Bei gemischten Plus- und Malketten
  

• Hier können Klammern einen Unterschied machen.
  

Name

• Die Klammern verbinden Zahlen miteinander.
  

• Die verbundenen Zahlen sind rechnerisch enger beieinander.
  

• Gemeinschaft erzeugen heißt auf Latein assoziieren.
  

• Daher das Wort Assoziativgesetz
  

Synonyme

• Assoziativgesetz ↗
  

• Verbindungsgesetz ↗
  

• Verknüpfungsgesetz ↗
  

• Klammergesetz ↗
  

Fußnoten

• [1] Lehr- und Übungsbuch Mathematik. Band I. Verlag Harri Deutsch. Thun und Frankfurt/Main. 20. Auflage. 1989. ISBN: 3 871 44 401 4. Dort heißt es auf Seite 46: "Summanden können in beliebiger Reihenfolge zu Teilsummen verbunden werden". Als Beispiel wird angeführt, dass (a+b)+c = a+(b+c) ist.
  

• [2] Lehr- und Übungsbuch Mathematik. Band I. Verlag Harri Deutsch. Thun und Frankfurt/Main. 20. Auflage. 1989. ISBN: 3 871 44 401 4. Dort heißt es auf Seite 55: "Faktoren können in beliebiger Reihenfolge zu Teilprodukten verbunden werden". Als Beispiel wird angeführt, dass (2·3)·5 = 2·(3·5) = 3·(2·5) ist.
  

• [3] Mathematik heute 5. Realschule. Schroedel Diesterweg Verlag. Braunschweig. 2005. ISBN: 3-507-87805-4. Dort auf Seite 92: "In einer Summe aus drei oder mehr Zahlen darf man Klammern beleibig setzen oder weglassen. Dabei ändert sich der Wert der Summe nicht." Sowie: "In einem Produkt aus drei odre mehr Zahlen darf man Klammern beliebig setzen oder weglassen. Dabei ändert sich der Wert des Produktes nicht."
  

• [4] In der Physik kann man auch die Assoziativität von mehr als zwei hintereinander ausgeführten Operationen untersuchen. Speziell zur sogenannten Superposition, das heißt der Überlagerung von Zuständen im Sinne der Quantenphysik heißt es: "The usual algebraic axioms of addition are assumed to hold, i. e. the commutative axiom c₁ψ₁ + c₂ψ₂ = c₂ψ₂ + c₁ψ₁ and the associative axiom (c₁ψ₁ + c₂ψ₂) + c₃ψ₃ = c₁ψ₁ + (c₂ψ₂ + c₃ψ₃). The first of these axioms implies that superposition of two states is a symmetrical process between them, which is obvious from the definition of §6, while the second implies the theorem, which was proved in §6, that in successive superpositions the order is unimportant." In: Paul Dirac: The Principles of Quantum Mechanics. Oxford University Press. 1930. Siehe auch Symmetrie (Physik) ↗