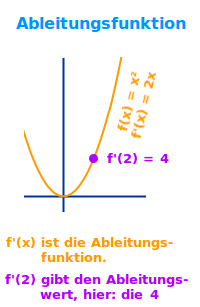
Ableitungsfunktion
f'(x)
© 2016
- 2025
Definition
Als Ableitungsfunktion f'(x) bezeichnet man eine Funktion deren y-Wert die Steigung der ursprünglichen Funktion f(x) angibt. Das wird hier erklärt.
Schritt-für-Schritt
- f(x) ist die eigentliche Funktion, z. B. f(x)=x²
- f'(x) ist die Ableitung von f(x), hier wäre f'(x)=2x.
- Man kann nun irgendeinen x-Wert in die Ableitungsfunktion einsetzen.
- Beispiel f'(3) = 2·3 = 6.
- Die Zahl 6 ist der y-Wert der Ableitungsfunktion bei x=3.
- Der y-Wert der Ableitungsfunktion ist gleichzeitig die Steigung von f(x).
- Bei x=3 hat die ursprüngliche Funktion f(x)=x² also die Steigung 6.
- Die Ableitungsfunktion f'(x) nennt man auch die erste Ableitung.
- Mehr zur Berechnung unter Steigung über erste Ableitung ↗
Merksatz
- Die Ableitungsfunktion f'(x) gehört immer zu einer Funktion f(x).
- Der y-Wert von f'(x) gibt für jeden x-Wert die Steigung von f(x).
Bedeutung
- Man sagt zum Beispiel: f(x)=x² abgeleitet an der Stelle x=4 gibt 8.
- Das meint: man geht auf den Punkt mit dem x-Wert 4: also (4|16).
- Dort hat die Parabel von f(x)=x² die Steigung 8.
- Mehr dazu unter Steigung in einem Punkt ↗
Fußnoten
- [1] Ableitungsfunktion kurzgefasst als Ableitung: Das Spektrum Lexikon der Mathematik, online, Stand 13. September 2021: https://www.spektrum.de/lexikon/mathematik/ableitung-einer-funktion/499 Spektrum Lexikon der Mathematik ↗
- [2] Ableitungsfunktion kurzgefasst als Ableitung: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Seite 446. Siehe auch Der Bronstein ↗