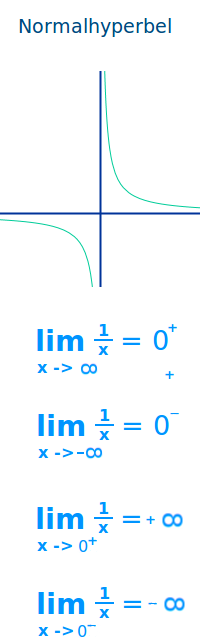Basiswissen

Wohin geht das?

• Limes ist ein anderes Wort für Grenzwert ↗
  

• Limes wird vor allem in einer besonderen Schreibweise benutzt.
  

• Als Erklärbeispiel dient hier die Normalhyperbel ↗
  

Limes

• Das Wort Limes meint "Grenzwert von"
  

• Man spricht: "Der Grenzwert von ..."
  

• Oder: "Limes von"
  

f(x)

• Nach dem Wort Limes steht entweder f(x)...
  

• oder ein wirklicher Funktionsterm, wie etwa 1/x.
  

• Im Beispiel hier nehmen wir f(x)=1/x
  

• Man spricht jetzt: "Der Grenzwert von f(x)..."
  

• Oder: "Der Grenzwert von eins durch x..."
  

x ⭢ ∞

• Unter dem Wort Limes steht: x ⭢ ∞
  

• Man liest: der Limes von x gegen unendlich
  

• Das heißt: man setzt gedanklich für x immer größere Zahlen ein.
  

• Man beoachtet dann, in welche Richtung sich die dazugehörigen y-Werte verändern.
  

• Möglichkeiten:
  

• a) Der y-Wert geht Richtung unendlich groß.
  

• b) Der y-Wert geht Richtung minus unendlich.
  

• c) Der y-Wert geht Richtung einer festen Zahlen.
  

• Beispiele:
  

• a) Limes von 1/x für x ⭢ ∞ = 0
  

• b) Limes von x² für x ⭢ ∞ = ∞
  

• c) Limes von 4-1/x für x ⭢ ∞ = 4
  

x ⭢ -∞

• Unter dem Wort Limes steht: x ⭢ -∞
  

• Man liest: der Limes von x gegen minus unendlich
  

• Das heißt: man setzt gedanklich für x immer kleinere Zahlen ein.
  

• Man beoachtet dann, in welche Richtung sich die dazugehörigen y-Werte verändern.
  

• Möglichkeiten:
  

• a) Der y-Wert geht Richtung unendlich groß.
  

• b) Der y-Wert geht Richtung minus unendlich.
  

• c) Der y-Wert geht Richtung einer festen Zahlen.
  

• Beispiele:
  

• a) Limes von 1/x für x ⭢ -∞ = 0
  

• b) Limes von x² für x ⭢ -∞ = ∞
  

• c) Limes von 4-1/x für x ⭢ -∞ = 4
  

x ⭢ z

• Unter dem Wort Limes steht: x ⭢ z
  

• Man liest: der Limes von x gegen z (z. B. 4 oder 5)
  

• Das heißt: man gedanklich immer dichter an die Zahl z heran, in immer kleineren Schritten.
  

• Man beoachtet dann, in welche Richtung sich die dazugehörigen y-Werte verändern.
  

• Möglichkeiten:
  

• a) Der y-Wert geht Richtung unendlich groß.
  

• b) Der y-Wert geht Richtung minus unendlich.
  

• c) Der y-Wert geht Richtung einer festen Zahlen.
  

• Beispiele:
  

• a) Limes von 1/x für x ⭢ 4 = 0,25
  

• b) Limes von x² für x ⭢ 4 = 16
  

• c) Limes von 4-1/x für x ⭢ 4 = 3,75
  

Fußnoten

• [1] 1860, Limes als Grenze: "Limes (lat.), 1) Grenze, Quergang durch die römischen Filiale von Osten nach Westen; daher 2) L. imperii romani, die befestigte Grenz- u. Vertheidigungslinie der Römer in Deutschland vom Niederrhein bis zur Donau." In: Pierer's Universal-Lexikon, Band 10. Altenburg 1860, S. 382-383. Online: http://www.zeno.org/nid/20010348107
  

• [2] Limes als Grenzwert im Sinn der Mathematik ist seit spätestens dem Jahr 1905 in Gebrauch: "Limes (lat., »Grenze«), in der Mathematik soviel wie Grenzwert." In: Meyers Großes Konversations-Lexikon, Band 12. Leipzig 1908, S. 557. Online: http://www.zeno.org/nid/20007004249