Basiswissen

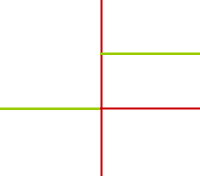
Die Heaviside-Funktion ist links von der y-Achse identisch mit der x-Achse. Für x>0 und auch x=0 selbst ist der Graph eine horizontale Gerade parallel zur x-Achse mit y=1. Diese Funktion hat überalle die Steigung 0, also ist auch f'(x) überall 0. Lediglich an der Stelle x=0 hat die Funktion eine Sprungstelle und ist deshalb dort nicht ableitbar. Diese Gegebenheiten sind im Folgenden noch einmal zusammengefasst:

Bildbeschreibung und Urheberrecht — Man sieht den Graphen der Heaviside-Funktion☛

f(x): alle Zahlen kleiner Null werden zu 0, alle anderen zu 1

Ableitung: f'(x) = 0

Außer: für x gleich 0 ist die Ableitung nicht definiert.

Bei x=0 hat die Funktion eine Sprungstelle.

Sprungstelle heißt: nicht differenzierbar.