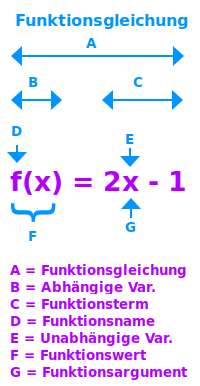
Funktionsgleichung
f(x)=Funktionsterm
Basiswissen
f(x) = 2x-5 - Hier steht eine kurze Erklärung der Bestandteile einer Funktionsgleichung: Name, Wert, Argument, Term, unabhängige und abhängige Variable.
Genereller Aufbau
- Links steht f(x) oder y
- Dann kommt das Gleichzeichen.
- Rechts steht dann der Funktionsterm.
- Das Ganze ist die Funktionsgleichung.
Bestandteile
- f(x) = 2x-1
- f ist der Funktionsname ↗
- x ist die unabhängige Variable ↗
- f(x) ist die abhängige Variable ↗
- f(x) ausgerechnet ist ein Funktionswert ↗
- Eine Zahl für x eingesetzt ist ein Funktionsargument ↗
- Die rechte Seite insgesamt ist der Funktionsterm ↗
f(x) oder y?
- Beides ist üblich und korrekt - auch an Hochschulen.
- f(x) betont mehr den Funktionsgedanken.
- y kann auch ohne Funktion stehen.
- Lies mehr unter y oder f(x) ↗
Beispiele
Muss immer ein x vorkommen?
- Das x heißt Variable.
- Statt dem x kann es auch jeder andere Buchstabe sein.
- Auch das wäre eine Funktionsgleichung: f(t)=t²-2t+1
Kann es auch gar keine Variable geben?
- Ja, es gibt auch Funktionsterme ganz ohne Variable.
- So eine Funktion nennt man konstante Funktion ↗
- Beispiel: f(x)=14