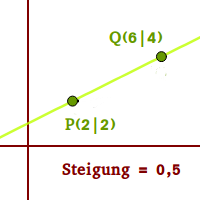
Steigung aus zwei Punkten
Geraden
© 2016
- 2025
Basiswissen
Man hat zwei Punkte auf einer Geraden gegeben, zum Beispiel die Punkte (2|2) und (6|4). Zwischen zwei Punkten kann man sich immer ein gerade Verbindungsstrecke denken. Für diese Verbindung kann man immer eine Steigung berechnen. Die Steigung zwischen diesen zwei Punkten hier im Beispiel 0,5. Man nennt sich auch die durchschnittliche Steigung. Hier wird erklärt, wie man diese Steigung berechnet.
Was muss man wissen?
- Die linken Zahlen in den Klammern sind die x-Werte.
- Die rechten Zahlen in den Klammern sind die y-Werte.
- Die x-Werte sagen, wie weit rechts von der y-Achse der Punkt liegt.
- Die y-Werte sagen, wie hoch über der x-Achse ein Punkt liegt.
- Punkte links von der y-Achse haben negative x-Werte.
- Punkte unter der x-Achse haben negative y-Werte.
Was meint Steigung hier?
- Die Steigung ist die Steilheit einer Geraden.
- Gerade meint hier den Graphen einer linearen Funktion.
- Die Steigung wird oft mit einem kleinen m abgekürzt.
Wie wird sie berechnet?
- Man rechnet den y-Wert vom Punkt rechts minus den y-Wert vom Punkt links.
- Dieses Ergebnis heißt Differenz der y-Werte oder kurz: Delta-y
- Delta ist ein mathematisches Fachwort und heißt Differenz oder Unterschied.
- Im Rechenbeispiel hier wäre Delta-y also 4-2 = 2.
- Dann rechnet man den x-Wert vom rechten Punkt minus den x-Wert vom linken Punkt.
- Das Ergebnis heißt Differenz der x-Werte oder kurz: Delta-x
- Im Rechenbeispiel wäre Delta-x 6-2 also 4.
- Dann rechnet man Delta-y geteilt durch Delta-x.
- 2/4 gibt 0,5. Das ist die Steigung.
- Also: Steigung m=0,5.