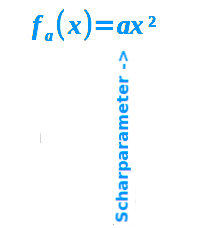Basiswissen

fₖ(x)=k·x²: das kleine k ist hier der Scharparameter: der Scharparameter ist ein Platzhalter, für den man eine bestimmte konstante Zahl einsetzt. Dadurch ist dann eine konkrete Funktionsgleichung entstanden. Innerhalb dieser Funktionsgleichung sind dann x und y - oder f(x) - die Variablen. Scharparameter treten auch im Zusammenhang mit Ebenen in der Vektorrechnung auf. Beides ist hier kurz erklärt.

Bildbeschreibung und Urheberrecht — Man sieht man die Schargleichung fa(x)=ax²☛

Scharparameter in der Analysis

Der Begriff Scharparameter gehört zum Thema Kurvenschar ↗

Scharparameter werden oft mit einem tiefgestellten Buchstaben abgekürzt, z. B.: ₐ ₖ ₗ ₘ ₙ ᵣ ₛ ₜ ᵤ ᵥ

Ein Scharparameter ist an sich eine Variable: ein Platzhalter für verschiedene Zahlen.

Aber: man möchte für bestimmte Betrachtungen diese Variable konstant halten.

Bei der Funktion fₖ(x)=k·x² könnte man zunächst nur k=2 betrachten: f(x)=2·x²

Für diese Betrachtung ist k dann konstant, nämlich 2.

Variablen, die man für Einzelfälle als konstant annimmmt, ...

während eine andere Varialbe (hier das x) variabel bleicht, ...

nennt man einen Scharparameter.

Siehe auch Kurvenschar ↗

Scharparameter in der Vektorrechnung

In der Vektorrechnung, auch analytische Geometrie oder lineare Algebra genannt, werden unter anderem auch Scharen von Ebenen oder Geraden behandelt. Diese Geraden und Ebenen werden meist in einem dreidimensionalen Koordinatensystem mit x-, y- und z-Achse gedacht. Kommt in der Gleichung ein Parameter vor, steht die Gleichung nicht nur für eine Gerade oder Ebene sondern meist für unendlich viele, die aber alle oft sehr ähnliche Eigenschaften haben. Lies als Beispiel dazu Ebenenschar ↗