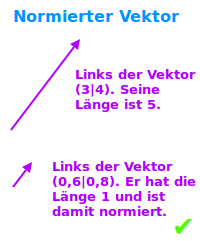
Normierter Vektor
Länge 1
Basiswissen
Ein normierter Vektor, auch Einheitsvektor genannt, ist ein Vektor dessen Länge genau 1 beträgt. Eine häufige Schreibweise ist â, also mit einem Zirkumflex (Dach) über dem Platzhalter. Der Vektor â = (1|0|0) beispielsweise ist normiert. Dazu hier mehr.
Beispiele
- Der Vektor (1|0|0) hat eine Länge von genau 1, er ist also normiert.
- Der Vektor (0|0,8|0,6) hat ebenfalls die Länge 1 und ist normiert.
- Mehr Beispiele unter normierte Vektoren ↗
Schreibweise
- Ein normierter Vektor wird oft mit einem kleinen lateinischen Buchstaben mit Dach abgekürzt.
- Der Vektor (1|0|0) kann z. B. geschrieben werden als â, û, v̂ oder auch ê.
- Das Dach heißt Caret oder auch Zirkumflex ↗
Vektorlänge
Die Länge eines Vektors, auch Vektorbetrag genannt, ist die Wurzel aus der Summe der Quadrate der einzelnen Vektorkomponenten. Der Vektor (1|2|3) hat die Länge Wurzel aus (1²+2²+3²), also Wurzel aus 14. Der Vektor (0,8|0,6|0) hat die Länge: Wurzel aus (0,8²+0,6²+0²), was ausgerechnet 1 ergibt. Mehr dazu unter Vektorlänge ↗
Berechnung
Man kann jeden beliebigen Vektor - außer dem Nullvektor - normieren und damit auf die Länge 1 bringen. Dabei ist der normierte Vektor immer kollinear zum Ausgangsvektor und der Pfeil zeigt in dieselbe Richtung wie vorher. Zur Normierung teilt man jede Komponente eines Vektors einzeln durch die Vektorlänge. Mehr unter Vektor normieren ↗
