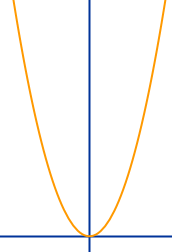
Normalparabel
Der Graph zu y = x²
Definition
Die Normalparabel ist der Graph von f(x)=x². Statt f(x) wird oft auch y geschrieben, das meint dasselbe. Die Funktion f(x) = x² heißt auch Quadratfunktion.
Aussehen
- Die Normalparabel ist immer nach oben geöffnet.
- Ihr Scheitelpunkt (tiefster Punkt) ist immer bei (0|0).
- Sie geht immer durch die Punkte (-1|1) und (1|1).
- Sie ist achsensymmetrisch zur y-Achse.
Was meint verschobene Normalparabel?
- Das ist eine Parabel mit genau derselben Form wie die Normalparabel.
- Aber sie liegt an einer anderen Stelle im Koordinatensystem.
- Sie hat also den Scheitelpunkt nicht bei (0|0).
- Aber sie ist immer nach oben geöffnet.
Was meint gespiegelte Normalparabel?
- Das ist eine Parabel mit genau derselben Form wie die Normalparabel.
- Aber anstatt nach oben ist sie nach unten geöffnet.
- Ihr Scheitelpunkt liegt auch in (0|0).
