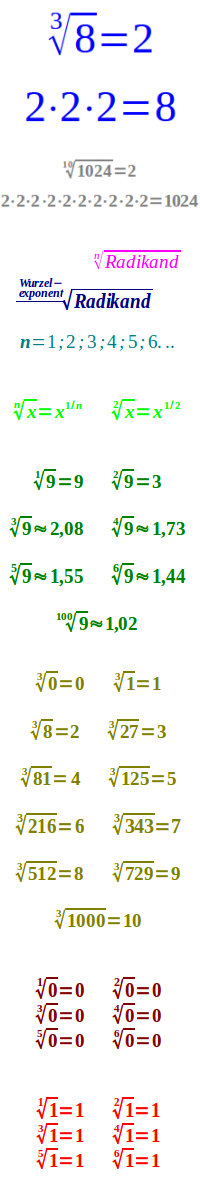n-te Wurzel
Mathematik
© 2016
- 2025
Definition|
Beispiele|
n|
Sprechweisen|
Berechnung|
Verallgemeinerung hin zur r-ten Wurzel|
Fußnoten
Definition
Die n-te Wurzel aus einer Zahl x, ist die Zahl, die n mal in einer Malkette stehen muss, dass x herauskommt.
Beispiele
- Die 1-te Wurzel von 4 wäre 4, weil 4 selbst 4 ist.
- Die 2-te Wurzel von 9 ist 3, weil 3·3 wieder 9 gibt.
- Die 3-te Wurzel von 64 ist 4, weil 4·4·4 wieder 64 gibt.
- Die 4-te Wurzel von 81 ist 3, weil 3·3·3·3 wieder 81 gibt.
n
- Das n steht für eine beliebige natürliche Zahl.
- Natürlich sind z. B. die 1; 2; 3; 4; 25; 26 und so weiter.
- [Die 0 gehört nicht zu den natürlichen Zahlen.]
Sprechweisen
- Die "erste Wurzel" von x ist x selbst.
- Die zweite Wurzel nennt man auch die Quadratwurzel ↗
- Die dritte Wurzel nennt man auch die Kubikwurzel ↗
- Die vierte Wurzel nennt man nur die vierte Wurzel ↗
Berechnung
- Bei vielen Zahlen nur überschlägig oder mit Taschenrechner.
- Bei manchen Zahlen geht es aber auch schnell im Kopf.
- Es hilft eine immer gleiche Rechenfrage:
- Die dritte Wurzel von 8 "erfragt" man so:
- Was muss 3mal in einer Malkette stehen, dass 8 herauskommt?
Verallgemeinerung hin zur r-ten Wurzel
Die n-te Wurzel[1] einer Zahl z kann man sich anschaulich als diejenige Zahl vorstellen, die n mal als Faktor in einer Malkette stehen muss, dass der Wert der Malkette, das rechnerische Produkt, genau die Zahl z ergibt.[2] Diese Vorstellung versagt, wenn man nach der 1,5ten Wurzel oder der ½ten Wurzel fragt. Die 1,5te Wurzel von der Zahl 8 etwa müsste dann 1,5 mal in einer Malkette stehen, um die Zahl 8 zu ergeben. Das macht keinen Sinn. Tatsächlich ist die 1,5te Wurzel von der 8 die Zahl 4. Wie man durch eine Verallgemeinerung der Idee der Wurzel dazu kommt, ist erklärt im Artikel über die r-te Wurzel ↗
Fußnoten
- [1] Der Ausdruck nte Wurzel ist verwendet in: "Die Berechnung dieser positiven Zahl heißt Ausziehen der nten W. aus a (Radizieren) und erfolgt am raschesten mit Hilfe der Logarithmen (s. Logarithmus), die man außer im Falle n = 2 stets benutzt." In:
- [2] "Wurzel, in der Mathematik die Zahl, die man durch Zerlegung einer gegebenen Zahl, des Radikanden, in mehrere gleich große Faktoren erhält; die Anzahl dieser Faktoren heißt der Wurzelexponent, und nach ihr wird die W. benannt." In: Meyers Großes Konversations-Lexikon, Band 20. Leipzig 1909, S. 796-797. Online: http://www.zeno.org/nid/20007709129