A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

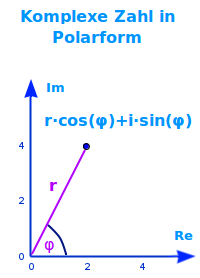
Komplexe Zahl in Polarform

r·cos(φ)+i·sin(φ)

© 2016 - 2025


Basiswissen｜ Darstellungen｜ Legende｜ Umwandlungen｜ Anschauliche Deutung


Basiswissen


z = r · [ cos(phi) + i·sin(phi) ] oder auch geschrieben als r·cos(φ)+i·sin(φ) ist die Polarform einer komplexen Zahl. Diese Form ist hier kurz vorgestellt.



Bildbeschreibung und Urheberrecht
Eine komplexe Zahl allgemein dargestellt in ihrer Polarform: das r heißt der Betrag und ist anschaulich der Abstand der als Punkt gedachten komplexen Zahl vom Koordinatenursprung. Das kleine φ heißt Argument und ist der Winkel des Ortsvektors zum gedachten Punkt mit der reellen Achse.☛


Darstellungen


  • z = r · [ cos(phi) + i·sin(phi) ]
  • z = r·cos(φ)+i·sin(φ)

Legende


  • z = die komplexe Zahl
  • r = Betrag der Zahl, Abstand zum Ursprung
  • i = Imaginäre Einheit
  • phi = Argument der komplexen Zahl, Winkel zur x-Achse (gegen Uhrzeigersinn)

Umwandlungen



Anschauliche Deutung


Komplexe Zahl als Zeiger oder Ortsvektor gedacht: Ein Pfeil beginnt im Ursprung (0|0) der Gaußschen Zahleneben. Die Spitze zeigt auf einen beliebigen Punkt. Sowohl der Pfeil als Vektor als auch der Punkt können dann als Repräsentation der komplexen Zahl gedacht werden. Siehe auch Ortsvektor ↗