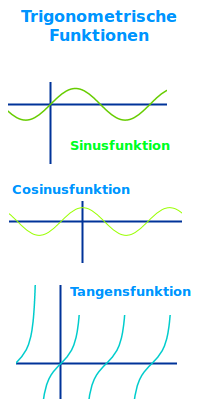
Trigonometrische Funktionen
Sinus, Cosinus, Tangens
Basiswissen
Die grundlegenden trigonometrischen Funktionen sind die Sinus-, Cosinus- und Tangensfunktion. Sie sind oft das mathematische Modell für periodische Vorgänge wie die Sonneeinstrahlung über die Jahreszeiten. Hier werden die Funktionen kurz vorgestellt.
Sinusfunktion
- Die Sinusfunktion hat die Gleichung: f(x) = sin(x)
- Die Sinusfunktion modelliert viele periodische Vorgänge.
- Der Graph ist eine Schlängellinie um die x-Achse.
- Für x kann man beliebige reelle Zahlen einsetzen.
- Der Graph ist punktsymmetrisch [zu (0|0)] ↗
- Die y-Werte schwanken zwischen -1 und 1.
- Mehr dazu unter Sinusfunktion ↗
Cosinusfunktion
- Die Cosinusfunktion hat die Gleichung: f(x) = cos(x)
- Die Cosinusfunktion modelliert zum Beispiel Wellen.
- Der Graph ist eine Schlängellinie um die x-Achse.
- Für x kann man beliebige reelle Zahlen einsetzen.
- Die y-Werte schwanken zwischen -1 und 1.
- Der Graph ist achsensymmetrisch zur y-Achse.
- Der Graph geht durch den Punkt (0|1).
- Mehr dazu unter Sinusfunktion ↗
Tangensfunktion
- Die Tangensfunktion hat die Gleichung: f(x) = tan(x)
- Eine größere Rolle spielt die Tangensfunktion in der Mechanik.
- Der Graph besteht aus vielen steil stehenden Einzelkurven.
- Für x kann man keine Vielfache von 90 Grad einsetzen.
- Die y-Werte schwanken minus und plus unendlich.
- Der Graph ist punktsymmetrisch zu (0|0)
- Der Graph geht durch den Punkt (0|0).
- Mehr dazu unter Tangensfunktion ↗
- Die Cosinusfunktion hat die Gleichung: f(x) = cos(x)
- Die Cosinusfunktion modelliert zum Beispiel Wellen.
- Der Graph ist eine Schlängellinie um die x-Achse.
- Für x kann man beliebige reelle Zahlen einsetzen.
- Die y-Werte schwanken zwischen -1 und 1.
- Der Graph ist achsensymmetrisch zur y-Achse.
- Der Graph geht durch den Punkt (0|1).
- Mehr dazu unter Sinusfunktion ↗
Tangensfunktion
- Die Tangensfunktion hat die Gleichung: f(x) = tan(x)
- Eine größere Rolle spielt die Tangensfunktion in der Mechanik.
- Der Graph besteht aus vielen steil stehenden Einzelkurven.
- Für x kann man keine Vielfache von 90 Grad einsetzen.
- Die y-Werte schwanken minus und plus unendlich.
- Der Graph ist punktsymmetrisch zu (0|0)
- Der Graph geht durch den Punkt (0|0).
- Mehr dazu unter Tangensfunktion ↗