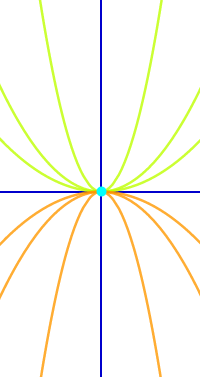
gemeinsamen Punkt einer Kurvenschar berechnen 6 Aufgaben mit Lösungen a) fₐ(x) = ax² c) fₜ(x) = x²+tx+1-t Man sieht ein blaues Koordinatensystem.☛ e) fₛ(x) = 0,1·[x³+2sx²+(6s−2)·x f) fₐ(x) = e^(2x)-a·e^x Lösungen Lösungen ==== zu den Aufgaben a) (0|0) b) (0|1) c) (1|2) d) (0|5) e) (0|0) und (-3|-2,1) f) kein gemeinsamer Schnittpunkt
