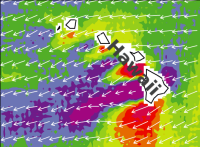
Vektorfeld
Mathematik
© 2016
- 2025
Definition|
Was ist ein Vektor an sich?|
Was ist ein Feld an sich?|
Felder aus Vektoren: das Vektorfeld|
Beispiele für Vektorfelder|
Vektoren ableiten: Vektoranalysis|
Fußnoten
Definition
Angenommen auf einer Wetterkarte ist für jeden Punkt auf der Erdoberfläche die Windrichtung mit einem Pfeil eingetragen. Die Länge des Pfeiles steht dabei für die Stärke des Windes. Diese Darstellung wäre ein Vektorfeld: für jeden Punkt eines Raumes (auch einer Ebene) ist ein Vektor zugeordnet.
Was ist ein Vektor an sich?
Ein Vektor ist anschaulich gesprochen ein Pfeil. Ein Vektor hat eine Länge und eine Richtung in die seine Spitze zeigt. Mit Vektoren kann man viele physikalische und mathematische Eigenschaften modellieren. So kann man die Bewegung von Luftteilchen (Wind) mit Vektoren angeben: die Pfeilspitze zeigt in Richtung der Bewegung, die Länge gibt die Geschwindigkeit an. Siehe auch 👉 Vektor [allgemein]
Was ist ein Feld an sich?
Man stelle sich ein Zimmer in einem Haus vor. Man kann für jeden Punkt in diesem Zimmer angeben, welche Temperatur dort gerade herrscht. Ordnet man jedem Raumpunkt dann seine Temperatur zu, hat man ein Temperaturfeld. Jede Zuordnung von Eigenschaften zu mehreren geometrischen Punkten nennt man in der Physik und Mathematik ein Feld. Siehe auch 👉 Feld [allgemein]
Felder aus Vektoren: das Vektorfeld
Man stelle sich ein Zimmer in einem Haus vor. Es ist Winter, die Heizung läuft auf vollen Touren. Dort wo die Heizungskörper angeordnet sind (oft nahe am Boden) steigt die Luft meist nach oben Richtung Zimmerdecke. An der Decke kühlt die Luft dann ab und sinkt an Wandteilen zu Boden, wo keine Heizkörper sind. Ordnet man jedem Punkt im Raum einen Vektor (Pfeil) zu, der angibt, in welche Richtung und mit welcher Geschwindigkeit sich die Luft dort bewegt, hat man ein 3D-Vektorfeld [1].
Beispiele für Vektorfelder
Die Schwerkraft an verschiedenen Stellen der Erde, also das Erdgravitationsfeld, die Felder um elektrisch geladene Körper, die Felder um Magnete oder auch der Wind an verschiedenen Punkten in der Atmosphäre sind typische Beispiele für 👉 Vektorfelder
Vektoren ableiten: Vektoranalysis
In der höheren Mathematik wird die Idee der Aufleitung mit der Idee von Vektoren und Feldern verbunden: man kann kann Ableitungen von Vektorfeldern bilden. Die Grundidee ist dabei, wie stark sich die Richtung oder Länge von Vektoren bei kleinen Veränderungen im Raum ändert. Siehe mehr dazu unter 👉 Vektoranalysis
Fußnoten
- [1] Der Bronstein definiert: "Wird jedem Punkt P eines Raumteiles ein Vektor V zugeordnet, so schreibt man V=V(P) und bezeichnet [diese Gleichung] als Vektorfeld." Im Original ist das V mit einer querliegenden Pfeil oben als Vektor gekennzeichnet. In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort das Kapitel 13.1.3. Vektorfelder. Seite 719.