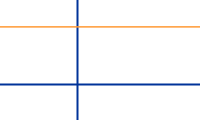
Konstante Funktion ableiten
f(x)=konstante Zahl gibt abgeleitet immer f'(x)=0
© 2016
- 2025
Basiswissen
Eine konstante Funktion hat als Graphen eine zur x-Achse parallel Gerade, also eine waagrechte (horizontal) Gerade. Die Steigung einer solchen Geraden ist für jede x-Stelle 0 (waagrecht). Daher ist auch der Funktionswert von f'(x) überall 0. Siehe auch Konstante Funktion ↗
Definition
- Eine Konstante Funktion ist ein Spezialfall einer ganzrationalen Funktion.
- Der Funktionswert f(x) ist immer gleich.
- Konstant meint: immer gleich
- Beispiel: f(x) = 10
Ableiten
- Die Ableitung ist immer 0.
- Es gilt: f'(x) = 0
- Und zwar immer.