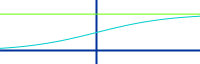
Sigmoidfunktion
Mathematik
Basiswissen
Flach liegendes S: eine Sigmoidfunktion steigt erst langsam, dann steil und dann wieder langsam an. Sie heißt auch Schwanenhalsfunktion.
Welche Eigenschaften hat die Sigmoidfunktion?
◦ ist für jede Zahl definiert (keine Definitionslücken)
◦ hat keine Sprünge im Graphen
◦ hat keine Knicke im Graphen
◦ ist also überall differenzierbar
◦ hat entweder überall positive Steigung...
◦ oder überall nur negative Steigung
◦ hat immer genau einen Wendepunkt
◦ hat immer eine obere Grenzen (höchsten Wert)
◦ und immer eine untere Grenze (tiefsten Wert)
◦ beinhaltet den Spezialfall logistischer Funktionen
Welche Rolle spielt sie in der KI?
◦ Sigmoidfunktionen werden bei der Programmierung neuronaler Netze verwendet.
◦ Mit ihnen kodiert man den Schwellenwert, ab wann ein Neurona feuert.
◦ Siehe auch => Neuronales Netz
Welche Rolle spielt sie in den Naturwissenschaften?
◦ Sie modelliert ähnliche Prozesse wie die Exponentialfunktion.
◦ Bei einer Exponentialfunktion "explodieren" die Funktioinswerte aber irgendwann.
◦ Das heißt: sie werden irgendwann immer größer und gehen gegegen unendlich.
◦ Bei einer Sigmoidfunktion flacht das Wachstum der y-Werte irgendwann ab.
◦ Man spricht von einer => Sättigungsfunktion
Beispiele
=> Tangens Hyperbolicus-Funktion
=> Arcustangensfunktion
=> Logistische Funktion
=> Fehlerfunktion
