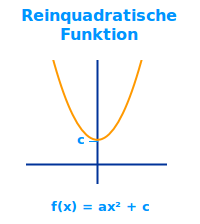
Reinquadratische Funktion
f(x) = ax² + c
Basiswissen
Der Funktionsterm hat immer ein quadratisches Glied (etwas mit x-quadrat). Dahinter darf - muss aber nicht ein + oder - mit absolutem Glied (eine reine Zahl ohne x) folgen.
Definition
- Die Funktionsgleichung kann immer umgeformt werden in:
- f(x) = ax²+c
Legende
- a darf irgendeine Zahl sein, außer der 0: a ∈ ℝ {0}
- c darf irgendeine Zahl sein, auch negativ oder 0: c ∈ ℝ
Beispiele
- f(x) = x²
- f(x) = 2x²
- f(x) = x² + 1
- f(x) = 4x² - 16
- f(x) = -2x² + 18
- f(x) = ax² + c
Begriffe
- Der Term mit dem x-quadrat heißt "quadratisches Glied".
- Der Term ohne x oder x-Quadrat heißt "absolutes Glied".
- a und c sind die Koeffizienten der Glieder.
Eigenschaften
- Der Graph heißt Parabel.
- Der Graph ist immer achsensymmetrisch zur y-Achse.
- Der Graph hat immer einen Scheitelpunkt.
- Der Scheitelpunkt liegt immer auf der y-Achse.
- Der Graph kann keine eine oder zwei Nullstellen (NS) haben.
- Die NS kann man immer über die pq-Formel finden (p ist dann 0)
- Die NS kann man immer über die ABC-Formeln finden.
- Die NS kann man immer über Umstellen-nach-x finden.