Rationale Funktion
Definition
Basiswissen
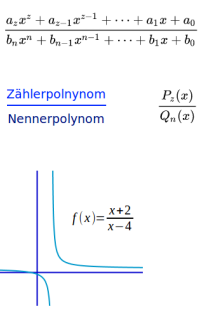
Jede Funktion, die man als Quotient aus zwei ganzrationalen Funktionen schreiben kann nennt man rational. Und nur solche Funktionen gelten als rational. Das ist hier kurz erklärt.
Eigenschaften
◦ Der Funktionsterm kann als Bruch mit Zähler (oben) und Nenner (unten) geschrieben werden.
◦ Der Zähler muss sich als ganzrationale Funktion schreiben lassen.
◦ Der Nenner muss sich als ganzrationale Funktion schreiben lassen.
Arten
=> Ganzrationale Funktion [x nur im Zähler]
=> Gebrochenrationale Funktion [x kann auch im Nenner sein]
Beispiele
◦ f(x) = 1/x
◦ f(x) = x/1
◦ f(x) = x/(x+1)
◦ f(x) = (x+1)/(x-2)
◦ f(x) = (4x^2 + 2x + 3)/(x^14 + x^9 - 3)
◦ Siehe auch => rationale Funktionen
