Krümmungsmaß
Funktionsgraphen
Basiswissen
Das Krümmungsmaß für einen Punkt auf einem Graphen einer Funktion ist definiert als der Kehrwert des Radius des Anschmiegekreises oder Krümmungskreises an diesen Punkt. Diese Krümmung κ ist nicht identisch mit der zweiten Ableitung einer Funktion. Das ist hier näher erklärt.
Definition
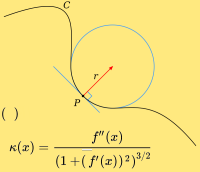
Man kann an jeden Punkt P eines differenzierbaren (stetig, ohne Knicke) Graphen einen sogenannten Anschmiege- oder Krümmungskreis anlegen. Das ist ein Kreis, der in der direkten Umgebung des Punktes dem Graphen am nächsten kommt. Je stärker ein Graph gekrümmt ist, desto kleiner ist dieser Kreis. Und je weniger stark ein Kreis gekrümmt, also je gerader er ist, desto größer ist der Radius dieses Kreises. Bei einer Geraden ist die Radius als unendlich angenommen. Als die Krümmung klein Kappa des Graphen an dem Punkt P definiert man den Kehrwert dieses Kreisradiusses.
Wie berechnet man das Krümmungsmaß?
Für eine gegebene differenzierbare Funktion f(x) berechnet man das Krümmungsmaß κ (klein Kappa) wie folgt: man schreibt zunächst einen langen leeren Bruchstrich auf. Der Zähler (oben) ist die zweite Ableitung f''(x). Der Nenner (unten) ist (1+(f'(x))²)^1,5, das heißt: der Nenner ist die Summe aus der Zahl Eins und dem Quadrat ersten Ableitung f'(x) und diese Summe dann hoch 1,5 gerechnet.
Unterschied zur qualititativen Krümmung
Das Krümmungsmaß wie oben definiert ist quantitativ, das heißt, man kann einen Zahlenwert für die Stärke angeben. Rein qualitativ, also ohne sinnvolle Zahlenangabe ist die Angabe, ob eine Graph an einer Stelle links- oder rechtsgekrümmt ist. Diese rein richtungsmäßige Angabe ist aber das einzige, dass die zweite Ableitung f''(x) einer Funktion zuverlässig angeben kann. Betrachtet man also nur die zweite Ableitung f''(x) einer Funktion, kann man damit bestimmen, bei welchen x-Werten ein Graph links- oder rechtsgekrümmt ist. Man kann damit aber nicht bestimmen, wie stark die Krümmung dort ausgeprägt ist. Als Beispiel kann man den Graphen von f(x)=e^x betrachten. Je weiter man nach rechts geht, desto gerader wird der Graph. Gleichzeitig steigt aber auch der Wert der zweiten Ableitung. Man sieht daran, dass eine größere zweite Ableitung nicht automatisch auch zu einem stärker gekrümmten Graphen passt. Lies mehr dazu unter schulmathematische Krümmung ↗
Verallgemeinerte Bedeutungen
Die Krümmung wurde hier zunächst für Funktionsgraphen in einem xy-Koordinatensystem definiert. Man kann die Krümmung aber auch für sogenannte Raumkurven, das sind Linien in einem xyz-Koordinatensystem oder sogar auch für Flächen angeben. In Lehrbüchern findet man mehr dazu unter dem Stichwort Krümmungsmaß.
Fußnoten
- [1] Franz Serafin Exner: Grundlagen der Naturwissenschaften. Deuticke Verlag. 1919. Dort wird ab Seite 18 das Krümmungsmaß K definiert als 1/rho, welches ursprünglich von Carl Friedrich Gauß eingeführt worden sei. Das kleine griechisch rho sei der Krümmungsradius, "das ist der Radius eines Kreises von gleicher Krümmung wie sie die Kurve an dem betreffenden Punkte besitzt". Exner lässt hier für rho auch den Wert unendlich zu, bei einem eindimensionalen Raum zu einer Gerade führt. Ist rho konstant (aber nicht unendlich), so entsteht ein Kreis. Für zweidimensionale Räume ergibt sich das Krümmungsmaß K als 1/(rho1 mal rho2). Rho1 und rho2 nennt Exner hier die Hauptkrümmungsradien. Sind sie beide unendlich groß, wird der zweidimensionale Raum zu einer "Ebene". Exner extrapoliert dann weiter in den dreidimensionalen Raum und definiert dessen Krümmungsmaß als 1/(rho1 mal rho2 mal rho3), und gesteht ein "Eine geometrische Vorstellung lässt sich damit freilich nicht mehr verbinden". Exner geht dann auf die geometrisch-physikalische Deutung spezieller Werte für K ein.