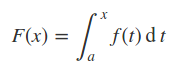Integralfunktion
Definition
Definition
Ein Integral, bei dem die linke (untere) Grenze als konstant und die rechte (obere) Grenze als variabel betrachtet wird nennt man eine Integralfunktion oder auch Flächenfunktion. Sie ist eine Form von einem unbestimmten Integral. Das ist hier weiter erklärt.
Definition
- Zu einer Funktion f(t) kann man oft eine Integralfunktion bilden.
- Man leitet f(t) auf und findet damit eine Stammfunktion.
- Die Integralfunktion schreibt man dann als F(x).
- Die untere linke Grenze ist dabei fest vorgegeben.
- Man schreibt die untere Grenze entweder als Zahl oder als Buchstabe.
- Der Buchstabe, oft ein a, steht aber immer für eine konstante Zahl.
- Die oberen rechte Grenze ist dann das x.
- Siehe auch Integrationsgrenzen ↗
Anschauliche Bedeutung
- Man kann in die Integralfunktion F(x) beliebige x-Werte einsetzen.
- Der Funktionswert von F(x) kann immer als konkrete Zahl berechnet werden:
- Der Zahlenwert ist die Flächenbilanz vom linken Rand bis zum eingegebenen x-Wert.
- Siehe auch Flächenbilanz ↗
Fußnoten
- [1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 436 ff. Der Papula ↗