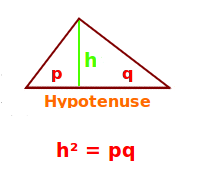
Höhensatz
Dreiecke
Basiswissen
h² = p·q ist der sogenannte Höhensatz. Er gilt für alle rechtwinkligen Dreieck und auch nur für rechtwinklige Dreiecke. Der Satz ist hier mit einem Rechenbeispiel erklärt.
Formel
- h² = p·q
Legende
- h = Höhe über der Hypotenuse [längste Seite im rechtwinkligen Dreieck] ↗
- p = ein Hypotenusenabschnitt [liegt immer auf der Hypotenuse]
- q = der andere Hypotenusenabschnitt [liegt auch auf der Hypotenuse]
Erklärung
h² meint h mal h. Die Höhe über der Hypotenuse c ist die Strecke, die senkrecht auf c steht und durch die Ecke mit dem rechten Winkel geht. p und q entstehen dadruch, dass die Höhe über der Hypotenuse, die Hypotenuse c in zwei Teile zerschneidet, eben p und q. Die Summe aus der Länge von p und der Länge von q ist immer gleich der Länge von c.
Wörtlich
- Multipliziere die Höhe über der Hypotenuse mit sich selbst.
- Multpliziere dann den einen mit dem anderen Hypotenusenabschnitt.
- Bei beiden Rechnungen muss immer dieselbe Zahl herauskommen.
Beispiele
- Man hat ein rechtwinkliges Dreieck mit der Seite c als Hypotenuse.
- Gegenüber dieser Hypotenuse liegt die Ecke C mit dem rechten Winkel.
- Die Höhe h über c geht senkrecht von c durch die Ecke C.
- Die Höhe h teilt die Hypotenuse in die Abschnitte p und q.
- Angenommen p ist 9 cm lang und q ist cm lang.
- Was ist dann die Höhe des Dreieckes?
- Rechnung: h² = p·q
- Mit p = 9 cm und q = 4 cm erhält man:
- h² = 9·cm·4·cm = 36 cm²
- Kurz: h² = 36·cm²
- Von beiden Seiten die Wurzel ziehen:
- h = 6 cm
- Die gesuchte Höhe ist 6 cm.
Gibt es noch alternative Formeln zur Höhe?
Ja, Höhen treten in vielen verschiedenen Zusammenhängen auf und oft gibt es dazu spezielle Höhenformeln ↗