Definitionsbereich
Definition
Basiswissen
Alle Zahlen, zu denen es einen y-Wert gibt: das Wort Definitionsbereich gehört normalerweise zu einer mathematischen Funktion. Der Definitionsbereich sind alle x-Werte denen die Funktion eindeutig einen y-Wert zuordnet. Der Definitionsbereich kann darüberhinaus aus sachlichen Gründen noch weiter eingeschränkt werden.
Definition
Bei Funktionen meint der Definitionsbereich alle x-Werte, zu denen es genau einen y-Wert gibt, für die die Funktion also definiert ist. x-Werte außerhalb des Definitionsbereiches werden nicht betrachtet. Allgemein ist der Definitionsbereich eine Menge von Elementen (Dingen), über die man eine Aussage trifft oder für die man eine Eigenschaft definiert.
Beispiele
- Man betrachte die Aussage: malrechnen macht das Ergebnis nie kleiner.
- Als Definitionsbereich legt man fest: alle natürlichen Zahlen.
- Für die natürlichen Zahlen (1; 2; 3 etc.) ist die Aussage immer wahr.
Begrenzung
- Man betrachte die Aussage: malrechnen macht das Ergebnis immer größer.
- Als Definitionsmeng legt man fest: alle natürlichen Zahlen ohne die 1.
- Die 1 macht das Ergebnis nicht größer als die Ausgangszahl.
- Deshalb nimmt man sie aus dem Definitionsbereich heraus.
Funktionen
- Definitionsbereiches spielen bei Funktionen eine wichtige Rolle.
- Hier meint Definitionsbereich: alle für x erlaubten Werte.
- Der Definitionsbereich wird abgekürzt mit einem großen D.
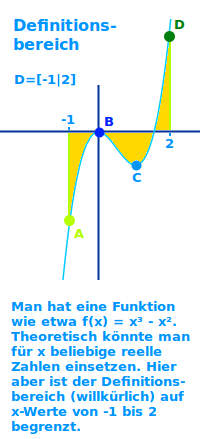
- Beispiel: f(x)=x³-x² mit D = {-1 < x < 2}
- Man darf für x Werte von -1 bis 2 einsetzen.
Definitionsbereich für Graphen
Eine Funktion hat nur innerhalb des Definitionsbereiches einen Graphen. Ist zum Beispiel f(x) = x² nur definiert für x-Werte zwischen 1 bis 3, dann wird auch der Graph nur von x=1 bis x=3 gezeichnet.
Definitionslücke
- Als Definitionslücke bezeichnet man "verbotene" Elemente.
- Die Funktion f(x)=1:x ist nicht definiert für x=0.
- Grund: 1:0 ist verboten, siehe unter durch 0 ↗
- Weitere Beispiele unter Definitionslücken ↗
Schreibweisen von Definitionsbereichen
- Als Abkürzung verwendet werden das D und das D mit doppelten Strich:
- D = [-1|2] = -1 und 2 gehören dazu beidseitig geschlossenes Intervall ↗
- D = ]-1|2[ = die -1 gehört nicht dazu beidseitig offenes Intervall ↗
- D = ]-1|2] = die -1 gehört nicht dazu linksoffenes Intervall ↗
- D = ]-1|2] = die 2 gehört dazu rechtsoffenes Intervall ↗
- D = [-1|2[ = die 2 gehört nicht dazu rechtsoffenes Intervall ↗
- D = N meint alle natürliche Zahlen ↗
- D = R meint alle reelle Zahlen ↗
- D = R {} meint alle rellen Zahlen ohne die 0
- D = {3; 7; -5; 20} meint die aufgelisteten Zahlen
- D = {x | x<5} meint: x derart dass x kleiner ist als 5
- D = {x | 2
- Mehr unter Mengenschreibweisen ↗