Blitzblick
Grundschulrechnen
Basiswissen
Mengen und Muster auf einen Blick erfassen nennt man Blitzblick, Fremdworte dafür sind Subitizing und Simultanerfassung. Wesentlich ist, dass man nicht Schritt für Schritt zählt. Der bewusst genutzte Blitzblick ist eine Zählstrategie. Hier stehen Beispiele dazu.
Was meint das?
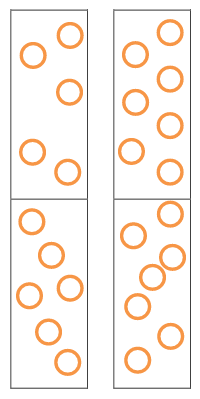
- Beim Blitzgucken oder Blitzblick bekommt man eine Menge von Dingen gezeigt.
- Das können zum Beispiel 9 Haselnüsse oder 25 Holzwürfel sein.
- Man kriegt die Dinge aber nur für einen Bruchteil einer Sekunde zu sehen.
- Die Dinge sind dazu hinter einer Holz- oder Pappwand verborgen.
- Die Wand wird dann ganz kurz hochgezogen und gibt den Blick frei.
- Die Anzahl sofort am Muster zu erkennen nennt man auch Subitizing ↗
Was ist der Sinn?
- Man trainiert a) innere Bilder im Kopf zu speichern.
- Man trainiert b) Mengen von Gegenständen zu strukturieren
- Man entlastet c) damit das Arbeitsgedächtnis ↗
Spielempfehlung
- Ein Kind spielt mit einem Erwachsenen.
- Man spielt nicht gegeneinander sondern miteinander.
- Erst legt der Erwachsene eine Menge und das Kind muss sie erkennen.
- Wer die Dinge hinlegt, hebt auch auch kurz die Wand an.
- Die Dinge waren gut gelegt, wenn der Mitspieler die Menge sofort erkennt.
- Wenn der Mitspieler die Menge nicht gut erkennt, dann waren die Dinge nicht gut gelegt.
- Nachdem der Erwachsene Dinge gelegt hat wird gewechselt, dann legt das Kind und hebt auch die Wand an.
- Während des Spielens gemeinsam probieren, mit welchen Anordungen man gut große Mangen erkennt.
Legetipps
- Bis zur Zahl 6 die Muster von Spielwürfeln werwenden
- Danach leicht erkennbare Kombinationen, z. B. 10 aus zwei 5ern
- Ab 20: Zehnerpakete gut sichtbar bündeln
- Selbst viel probieren. Die Frage ist immer:
- Wie kann man legen, dass der Mitspieler leicht die Zahl erkennt.
- Siehe auch Zahlenbilder ↗
Blitzblick und Dyskalkulie
Kinder mit einer Dyskalkulie tun sich mit einem Blitzblick oft schwer, wo andere Kinder sofort die richtige Anzahl erkennen. So zählte eine Schülerin aus der Klasse 2 Stück für Stück 3 Nüsse, wenn sie auf den Tisch gelegt wurden. Verschob man nach dem ersten Zähldurchgang eine der Nüsse geringfügig, so zählte sie neu. Es dauerte rund zwei Monate, bis sie zu der Einsicht gelangte, dass sich die Anzahl nicht verändert wenn die Nüsse etwas anders gelegt werden. Sie formulierte diese Einsicht mit klaren Worten und brachte ihre große Überraschung darüber zum Ausdruck. Was ihre fehlte, war eine intuitive Vorstellung der sogenannten Mengenkonstanz ↗