Anschaulich rechnen
Anleitungen
Basiswissen
Man unterscheidet anschauliches und formales rechnen. Wer formal rechnet folgt dabei Regeln ohne dass ein erkennbarer Bezug zu Größen, Längen oder Mengen nötig ist. Beim anschaulichen Rechnen hingegen stehen sinnlich wahrnehmbare Dinge im Mittelpunkt. Hier stehen einige Tipps dazu.
Subtrahieren als Abziehen
Aus 101-3 wird: ich habe 101 und ziehe drei ab. Wie bleibt am Ende übrig? Die Antwortist 98. Diese Rechenfrage nimmt man, wenn die Zahl vor dem Minuszeichen sehr viel größer ist als die Zahl nach dem Minuszeichen.
- Ab der Grundschule Abziehfrage ↗
- Mit Kommazahlen Abziehen ↗
Subtrahieren als Ergänzung
Aus 101-93 wird: man will 101 und hat 93. Wie viel fehlt noch? Die Anwort ist 8. Diese Rechenfrage ist von Vorteil, wenn beide Zahlen aus der Aufgabe ähnlich groß sind, der Unterschied als klein ist.
- Ab der Grundschule Ergänzungsfrage ↗
- Mit Kommazahlen Ergänzen ↗
Dividieren als Verteilung
Aus 12:4 wird die Rechenfrage: man hat 12 Eiskugeln und verteilt sie gleichmäßig auf 4 Kinder. Wie viele Kugeln kriegt jedes Kind? Die Antwort ist 3. Diese Rechenfrage nennt man auch die Verteilungsfrage.
- Ab der Grundschule Verteilungsfrage ↗
- Mit Kommazahlen Verteilungsdivision ↗
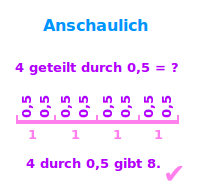
Dividieren als Aufteilung
Aus 12:4 wird die Rechenfrage: man hat 12 Eiskugeln. In wie viele Portionen mit je 4 Kugeln könnte man das aufteilen? Die Antwort ist 3. Diese Rechenfrage nennt man auch die Aufteilungs- oder Päckchenfrage.
- Aber der Grundschule Päckchenfrage ↗
- Mit Kommazahlen Päckchendivision ↗
Teilen mit Rest
- 10 geteilt durch 4 gibt 2 Rest 2.
- 10 geteilt durch 8 gibt 1 Rest 2.
- Mehr unter Teilen mit Rest ↗
Gemischte Zahlen
- Aufgabe: 1½ mal 20
- Frage: Was ist das Anderthalbfache von 20?
- Anders: wie viel ist ein Mal die 20 ganz und die Hälfte von 20 noch dazu? Antwort: 30
- Lies mehr unter Rechnen mit gemischten Zahlen ↗
Dezimaler Multiplikator
- 0,003 mal 4000
- Wie viel sind 3 Tausender von der 4000?
- Mehr unter Dezimalzahl als Multiplikator ↗
Wurzelziehen als Malkette
- Aufgabe: Was ist die vierte Wurzel aus 81?
- Frage: Was muss viermal in einer Malkette stehen, dass 81 rauskommt?
- Antwort: die Zahl 3. Lies mehr unter n-te Wurzel ↗
Logarithmieren als Hochzahl suchen
- Aufgabe: Was ist lg 1000?
- Frage: 10 hoch was gibt 1000? (Antwort: 3)
- Lies mehr unter Logarithmieren ↗
Einfache Gleichungen verbalisieren
- 3x=12 ⭢ Was steckt drei mal in der Zwölf? ⭢ 3 mal was gibt Zwölf? Antwort: 4
- 60:x=15 ⭢ Was steckt 15 mal in der 60? ⭢ Antwort: 4
- Siehe auch Gleichungen lösen über Probieren ↗
Gleichungssysteme lösen
- I: y=2x+4 und II y=1x+8
- Sprache: welches Pärchen von x und y löst beide Gleichungen gleichzeitig? Antwort: x=3 und y=12.
- Lies mehr unter LGS graphisch lösen ↗
Anschaulich formal ableiten
- Ableiten mit dx und dy kann man sich anschaulich vorstellen.
- Lies mehr dazu unter differenzieren ↗
Anschaulich formal aufleiten
- Aufleiten mit dx kann man sich anschaulich vorstellen.
- Lies mehr dazu unter Säulenmethode ↗
Graphisch ableiten
- Man hat zum Beispiel: f(x)=x²
- Wie sieht der Graph der Ableitungsfunktion f'(x) aus?
- Lies mehr unter graphisch ableiten ↗
Graphisch aufleiten
- Man hat eine Funktionsgleichung wie etwa: f(x)=x²
- Wie sieht der Graph der Aufleitungsfunktion F(x) aus?
- Lies mehr unter graphisch aufleiten ↗
Graphisch integrieren
- Man hat eine Funktionsgleichung wie etwa: f(x)=x²
- Gesucht ist die Fläche zwischen verschiedenen x-Werten (Intervall).
- Über ein Visualisierung kann man schnell einfache Abschätzung erhalten.
- Lies mehr unter anschaulich integrieren ↗
3D-Gerade visualisieren
- Man hat eine Geradengleichung mit Vektoren.
- Diese lässt sich leicht dreidimensional visualisieren.
- Lies unter Parameterform der Geraden anschaulich ↗
Vektoren visualisieren
- Vektoren kann man sich als Pfeile vorstellen.
- Oft werden sie in einem 3D-Koordinatensystem gedacht.
- Siehe dazu auch Kiste [Vektorstudio] ↗
Kieler Zahlenbilder
Die Kieler Zahlenbilder sind Figuren für die Zahlen 1 bis 10. Sie setzen sozusagen die Punktmuster eines Spielwürfels bis zur Zahl 10 fort. Die Kieler Zahlenbilder wurden vor allem für Kinder mit einer Dyskalkulie entwickelt. Aus der Erfahrung in der Mathe-AC Lernwerkstatt Aachen können wir sagen, dass Kinder damit sehr gerne arbeiten und den Zahlenraum bis 20 damit sehr gut erfassen können. Mehr unter Kieler Zahlenbilder ↗
Dienes Material
Einerwürfel, Zehnerstangen, Hunderterplatten und Tausenderwürfel: die Grundidee des Dienes Materials ist die Veranschaulichung von Zahlen mit kleinen Würfeln. In der Mathe-AC Lernwerkstatt Aachen hat sich das Dienes Material als hervorragend geeignet für Kinder mit und ohne Dyskalkulie erwiesen. Lies mehr unter Dienes Material ↗
Versuche
Temperaturen messen und gleichzeitig auch echt fühlen, Kräfte an Federn und Hebeln spüren oder Zeitdauern sinnlich fassbar machen: abstrakte Ideen wie zum Beispiel Länge, Kraft und Zeit können durch einfache Versuche sinnlich erfahrbar und damit be-greifbar gemacht werden. Die enge Verbindung von mathematischer Theorie und altersgerechter Veranschaulichung ist die Kernidee der Mathe-AC Lernwerkstatt Aachen ↗